并查集

介绍

作用

将两个集合合并
询问两个元素是否在一个集合中

基本原理

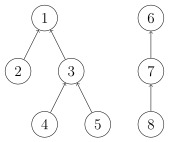
每一个集合用一课树来表示，树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点。

问题1： 如何判断树根：if(p[x] == x)

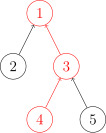
问题2： 如何求x的集合编号：while (p[x] != x) x = p[x]

问题3： 如何合并两个集合：px是x的集合编号，py是y的集合编号。p[x] = y

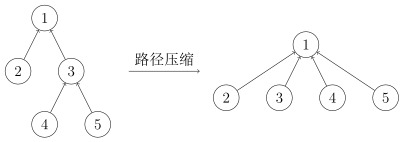
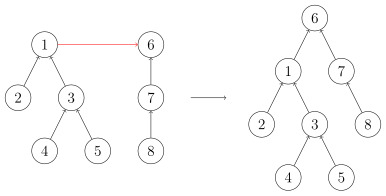
基本操作图解

两个集合

查询根节点

路径压缩

合并两个集合

解题模板

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108


(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);


(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);


(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量
堆 —— 模板题 AcWing 838. 堆排序, AcWing 839. 模拟堆
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);

作者：yxc

题目练习

第一题：合并集合

一共有 $n$ 个数，编号是 $1∼n$ ，最开始每个数各自在一个集合中。

现在要进行 $m$ 个操作，操作共有两种：

M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；

Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式

第一行输入整数 $n$ 和 $m$ 。

接下来 $m$ 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 $a$ 和 $b$ 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

$1≤n,m≤10^5$

输入样例：

输出样例：

1
2
3


Yes
No
Yes

参考答案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


#include <iostream>

using namespace std;

const int N = 100010;

int p[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    while (m -- )
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if (*op == 'M') p[find(a)] = find(b);
        else
        {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

第二题：连通块中点的数量

给定一个包含 $n$ 个点（编号为 $1∼n$ ）的无向图，初始时图中没有边。

现在要进行 $m$ 个操作，操作共有三种：

C a b，在点 $a$ 和点 $b$ 之间连一条边，$a$ 和 $b$ 可能相等；
Q1 a b，询问点 $a$ 和点 $b$ 是否在同一个连通块中，$a$ 和 $b$ 可能相等；
Q2 a，询问点 $a$ 所在连通块中点的数量；

输入格式

第一行输入整数 $n$ 和 $m$ 。

接下来 $m$ 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 $a$ 和 $b$ 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 $a$ 所在连通块中点的数量

每个结果占一行。

数据范围

$1≤n,m≤10^5$

输入样例：

输出样例：

参考答案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N], cnt[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++)
    {
        p[i] = i;
        cnt[i] = 1;
    }
    
    while(m --)
    {
        string op;
        int a, b;
        cin >> op;
        
        if (op == "C")
        {
            cin >> a >> b;
            a = find(a), b = find(b);
            if(a != b)
            {
                p[a] = b;
                cnt[b] += cnt[a];
            }
        }
        else if (op == "Q1")
        {
            cin >> a >> b;
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }
    
    return 0;
}

第三题：食物链

动物王国中有三类动物 $A,B,C$ ，这三类动物的食物链构成了有趣的环形。

$A$ 吃 $B$ ，$B$ 吃 $C$ ，$C$ 吃 $A$ 。

现有 $N$ 个动物，以 $1∼N$ 编号。

每个动物都是 $A,B,C$ 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 $N$ 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 $X$ 和 $Y$ 是同类。

第二种说法是 2 X Y，表示 $X$ 吃 $Y$ 。

此人对 $N$ 个动物，用上述两种说法，一句接一句地说出 $K$ 句话，这 $K$ 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 $X$ 或 $Y$ 比 $N$ 大，就是假话；
当前的话表示 $X$ 吃 $X$ ，就是假话。

你的任务是根据给定的 $N$ 和 $K$ 句话，输出假话的总数。

输入格式第一行是两个整数 $N$ 和 $K$ ，以一个空格分隔。

以下 $K$ 行每行是三个正整数 $D，X，Y$ ，两数之间用一个空格隔开，其中 $D$ 表示说法的种类。

若 $D=1$ ，则表示 $X$ 和 $Y$ 是同类。

若 $D=2$ ，则表示 $X$ 吃 $Y$ 。

输出格式

只有一个整数，表示假话的数目。

数据范围

$1≤N≤50000,$

$0≤K≤100000$

输入样例：

输出样例：

1

3

参考答案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61


#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N], d[N];

int find(int x)
{
    if (p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <=n; i ++) p[i] = i;
    
    int res = 0;
    while(m --)
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);
        
        if (x > n || y > n) res ++;
        else
        {
            int px = find(x), py = find(y);
            if (t == 1)
            {
                if (px == py && (d[x] - d[y]) % 3) res ++;
                else if (px != py)
                {
                    p[px] = p[y];
                    d[px] = d[y] - d[x];
                }
            }
            else 
            {
                if (px == py && (d[x] - d[y] - 1) % 3) res ++;
                else if (px != py)
                {
                    p[px] = p[y];
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    
    printf("%d\n", res);
    
    return 0;
}

在这段代码中，d[x] 数组用于记录每个节点相对于其根节点的关系偏移量。这个偏移量帮助我们在并查集中表达和判断复杂的关系（例如“同类关系”、“捕食关系”等）。d[x] 的引入是为了在路径压缩的过程中保持节点之间的相对关系，具体来说有以下几个原因：

1. 维护元素之间的相对关系

在这个题目中，d[x] 的值并不是一个简单的距离，而是一个编码，表示节点 x 与其根节点的关系类型。通常我们会使用数字编码来表示不同的关系类型，例如：

0 表示“同类”关系。
1 表示“x 捕食 y”关系。
2 表示“y 捕食 x”关系。

通过使用 d[x] 数组记录这些相对关系，可以更轻松地在不同节点之间传播这些关系，而不用单独处理每一对关系。

2. 在路径压缩中维护关系的一致性

在执行 find 函数时，为了压缩路径，节点 x 的父节点会被直接设置为其根节点。这一操作会改变节点的层次结构。此时，为了确保路径压缩不会影响原来的关系，代码使用 d[x] += d[p[x]]; 来更新节点 x 到根节点的关系，使得路径压缩后节点与根节点的关系依旧正确。

3. 用于判断矛盾 在合并不同集合或处理查询时，程序通过检查 d[x] 和 d[y] 的差值来判断两个节点之间的关系是否合理。例如：

1

if (px == py && (d[x] - d[y]) % 3 != expected_value)

这一判断通过 d[x] 和 d[y] 的差值来验证节点 x 和 y 是否满足给定的关系条件。如果不满足，则标记为矛盾。

代码示例分析

例如，当我们有一个查询表示“x 和 y 是同类”时，我们希望 d[x] 和 d[y] 的差值满足 (d[x] - d[y]) % 3 == 0。如果条件不满足，说明出现了矛盾关系。类似地，对于捕食关系的查询，条件会相应变化。

总结

d[x] 是为了维护并查集树结构中节点之间的关系信息而设置的，它记录了相对于根节点的偏移关系，并在路径压缩中调整该偏移量以保持关系的一致性。这种做法可以有效处理并查集中带有复杂关系的情况，尤其适用于关系传递和判断。

总结

理解并查集，一定要理解它的核心原理，还有常见的使用方法，并且能够迅速地把代码写出来。